专为高中生提供有价值的资讯
椭圆方程为x²/a²+y²/b²=1,对x求导可得:2x/a²+2yy'/b²=0,因此椭圆上任意一点(x,y)处的切线斜率k=y'=-b²x/(a²y);若M(x₀,y₀)为椭圆上任意一点,则过M的切线方程为:y=[-b²x₀/(a²y₀)](x-x₀)+y₀。


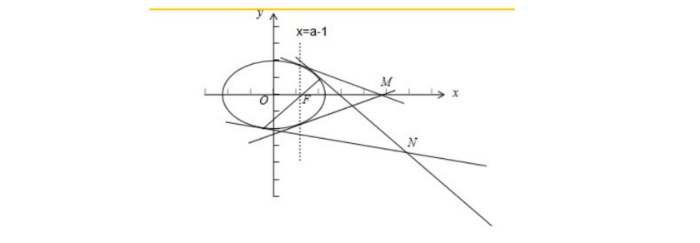
直线与椭圆的位置关系分为三种:相离、相切、相交。
1.直线与椭圆相离的充要条件是直线与椭圆的方程组成的方程组无解,即所得一元二次方程的根的判别式小于0。
2.直线与椭圆相切的充要条件是直线与椭圆的方程组成的方程组有唯一解,即所得一元二次方程的根的判别式等于0。
3.直线与椭圆相交的充要条件是直线与椭圆的方程组成的方程组有两个不同的解,即所得一元二次方程的根的判别式大于0。
Copyright 2019-2029 http://www.laigaokao.com 【来高考】 皖ICP备19022700号-4
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告