专为高中生提供有价值的资讯





 2023年高考数学模拟试卷01(浙江省)
2023年高考数学模拟试卷01(浙江省)
一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. )
)
1.(2022·吕梁模拟)已知集合A={x|x2-2x-3<0},B={x|log2x<2},则A∩B等于( )
A.(-1,4) B.(-1,3)
C.(0,3) D.(0,4)
2.(2022·长春模拟)已知复数z的共轭复数=,则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.(2022·重庆调研)函数y=ln cos x的图象是( )

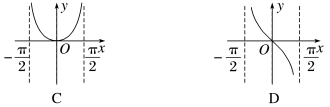
4.(2022·郑州模拟)如图,在五面体ABCDEF中,四边形ABCD是正方形,AB=4,EF=2,△BCF,△ADE都是等边三角形,则五面体ABCDEF的体积为( )

A. B.
C. D.4
5.函数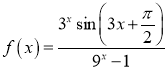 图像大致为( )
图像大致为( )
A. B.
B.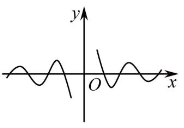
C. D.
D.
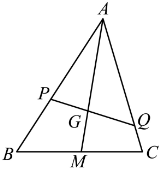
6.如图,在△ABC中,M为线段BC的中点,G为线段AM上一点且 ,过点G的直线分别交直线AB、AC于P、Q两点,
,过点G的直线分别交直线AB、AC于P、Q两点, ,
, ,则
,则 的最小值为( )
的最小值为( )
A.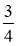 B.1 C.
B.1 C. D.4
D.4
7.已知椭圆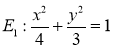 的右焦点为F,以椭圆
的右焦点为F,以椭圆 的长轴为直径作圆
的长轴为直径作圆 ,过点F作不与坐标轴垂直的两条直线
,过点F作不与坐标轴垂直的两条直线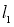 ,
, ,其中
,其中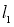 与椭圆
与椭圆 交于M,N两点,
交于M,N两点, 与圆
与圆 交于P,Q两点,若
交于P,Q两点,若 ,且都有
,且都有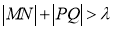 ,则实数
,则实数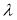 的取值范围为( ).
的取值范围为( ).
A. B.
B.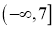
C. D.
D.
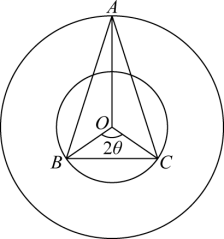
8.某单位科技活动纪念章的结构如图所示, 是半径分别为
是半径分别为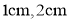 的两个同心圆的圆心,等腰三角形
的两个同心圆的圆心,等腰三角形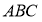 的顶点
的顶点 在外圆上,底边
在外圆上,底边 的两个端点都在内圆上,点
的两个端点都在内圆上,点 在直线
在直线 的同侧.若线段
的同侧.若线段 与劣弧
与劣弧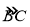 所围成的弓形面积为
所围成的弓形面积为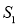 ,△
,△ 与△
与△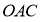 的面积之和为
的面积之和为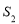 ,设
,设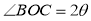 .经研究发现当
.经研究发现当 的值最大时,纪念章最美观,当纪念章最美观时,
的值最大时,纪念章最美观,当纪念章最美观时, ( )
( )
A.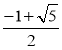 B.
B.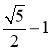 C.
C. D.
D.
二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. )
)
9.已知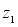 ,
, 均为复数,则下列结论中正确的有( )
均为复数,则下列结论中正确的有( )
A.若 ,则
,则 B.若
B.若 ,则
,则 是实数
是实数
C. D.若
D.若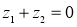 ,则
,则 是实数
是实数
10.有 个相同的球,分别标有数字
个相同的球,分别标有数字 ,
, ,
, ,
, ,
, ,
, ,从中有放回的随机取两次,每次取
,从中有放回的随机取两次,每次取 个球.记第一次取出的球的数字为
个球.记第一次取出的球的数字为 ,第二次取出的球的数字为
,第二次取出的球的数字为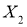 .设
.设 ,其中
,其中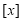 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
,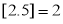 ,则( )
,则( )
A.
B.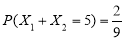
C.事件“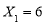 ”与“
”与“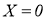 ”互斥
”互斥
D.事件“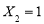 ”与“
”与“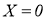 ”对立
”对立
11.取名于荷兰数学家鲁伊兹·布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理.该定理表明:对于满足一定条件的图象连续不间断的函数 ,在其定义域内存在一点
,在其定义域内存在一点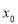 ,使得
,使得 ,则称
,则称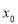 为函数
为函数 的一个不动点,那么下列函数具有“不动点”的是( )
的一个不动点,那么下列函数具有“不动点”的是( )
A. B.
B.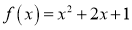
C. D.
D.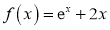
12.如图,正方体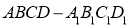 棱长为
棱长为 ,
, 是直线
是直线 上的一个动点,则下列结论中正确的是( )
上的一个动点,则下列结论中正确的是( )
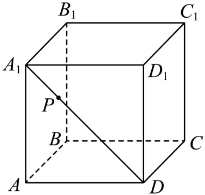
A. 的最小值为
的最小值为
B. 的最小值为
的最小值为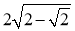
C.三棱锥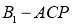 的体积不变
的体积不变
D.以点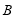 为球心,
为球心,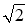 为半径的球面与面
为半径的球面与面 的交线长
的交线长
三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)
13.已知平面向量a,b满足a=(1,2),|b|=,a·b=,则cos〈a,b〉=________.
14.如图,在等腰直角 中,
中, ,
,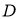 为
为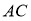 的中点,将线段
的中点,将线段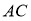 绕点
绕点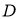 旋转得到线段
旋转得到线段 .设
.设 为线段
为线段 上的点,则
上的点,则 的最小值为___________.
的最小值为___________.

15.在线投标问题的定义是:商家给出一个足够大的正整数M,但投标者不知道M的值,故只能通过不断给出价格序列 来竞标,已知
来竞标,已知 ,
, .若正整数k使得
.若正整数k使得 ,则此次竞标投标者共花费
,则此次竞标投标者共花费 中标,我们的目标是对于任意足够大的正整数M,最小化竞争比
中标,我们的目标是对于任意足够大的正整数M,最小化竞争比 ,则当
,则当 ________.时,在线投标问题的竞争比最小.
________.时,在线投标问题的竞争比最小.
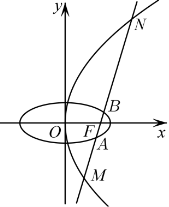
16.已知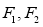 为双曲线
为双曲线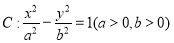 的左右焦点,过点
的左右焦点,过点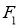 作一条渐近线的垂线交双曲线右支于点P,直线
作一条渐近线的垂线交双曲线右支于点P,直线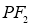 与y轴交于点Q(P,Q在x轴同侧),连接
与y轴交于点Q(P,Q在x轴同侧),连接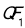 ,如图,若
,如图,若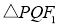 内切圆圆心恰好落在以
内切圆圆心恰好落在以 为直径的圆上,则
为直径的圆上,则 ________;双曲线的离心率
________;双曲线的离心率 ________.
________.

四、解答题(本题共6小题,共70分,其中第16题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤. )
)
17.设函数 ,数列
,数列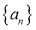 满足
满足 (
(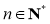 ,且
,且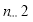 ).
).
(Ⅰ)求数列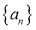 的通项公式;
的通项公式;
(Ⅱ)设 ,若
,若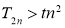 对
对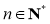 恒成立,求实数
恒成立,求实数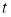 的取值范围.
的取值范围.
18.(12分)(2022·新余模拟)如图,在三棱锥P-ABC中,已知PA=PB=PC=AB=AC,E是PA的中点.

(1)求证:平面PAB⊥平面BCE;
(2)若BC=AB,求平面ABC与平面ABE夹角的正弦值.
19.在钝角 中,内角
中,内角 ,
,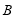 ,
, 的对边为
的对边为 ,
, ,
, ,已知
,已知 .
.
(1)若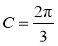 ,求
,求 ;
;
(2)求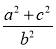 的取值范围.
的取值范围.
20.京东配送机器人是由京东研发,进行快递包裹配送的人工智能机器人. 年
年 月
月 日,京东配送机器人在中国人民大学顺利完成全球首单配送任务,作为整个物流系统中末端配送的最后一环,配送机器人所具备的高负荷、全天候工作、智能等优点,将为物流行业的“最后一公里”带去全新的解决方案.已知某市区
日,京东配送机器人在中国人民大学顺利完成全球首单配送任务,作为整个物流系统中末端配送的最后一环,配送机器人所具备的高负荷、全天候工作、智能等优点,将为物流行业的“最后一公里”带去全新的解决方案.已知某市区 年
年 到
到 月的京东快递机器人配送的比率图如图所示,对应数据如下表所示:
月的京东快递机器人配送的比率图如图所示,对应数据如下表所示:

|
|
|
|
|
|
时间代码 |
|
|
|
|
|
配送比率 |
|
|
|
|
|
(1)如果用回归方程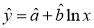 进行模拟,请利用以下数据与公式,计算回归方程;
进行模拟,请利用以下数据与公式,计算回归方程;
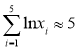 ,
,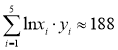 ,
,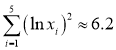 .
.
参考公式:若 ,则
,则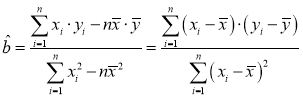
(2)已知某收件人一天内收到 件快递,其中京东快递
件快递,其中京东快递 件,菜鸟包裹
件,菜鸟包裹 件,邮政快递
件,邮政快递 件,现从这些快递中任取
件,现从这些快递中任取 件,
件, 表示这四件快递里属于京东快递的件数,求随机变量
表示这四件快递里属于京东快递的件数,求随机变量 的分布列以及随机变量
的分布列以及随机变量 的数学期望.
的数学期望.
21.已知抛物线G: 的焦点与圆E:
的焦点与圆E: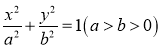 的右焦点F重合,椭圆E的短轴长为2.
的右焦点F重合,椭圆E的短轴长为2.
(1)求椭圆E的方程;
(2)过点F且斜率为k的直线l交椭圆E于A、B两点,交抛物线G于M,N两点,请问是否存在实常数t,使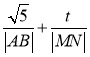 为定值?若存在,求出t的值;若不存在,说明理由.
为定值?若存在,求出t的值;若不存在,说明理由.
22.)(2022·潍坊模拟)已知函数f(x)=ex-ax-a,a∈R.
(1)讨论f(x)的单调区间;
(2)当a=1时,令g(x)=.
①证明:当x>0时,g(x)>1;
②若数列{xn}(n∈N*)满足x1=, =g(xn),证明:2n(
=g(xn),证明:2n(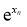 -1)<1.
-1)<1.

 学科网(北京)股份有限公司
学科网(北京)股份有限公司

 学科网(北京)股份有限公司
学科网(北京)股份有限公司
Copyright 2019-2029 http://www.laigaokao.com 【来高考】 皖ICP备19022700号-4
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告