专为高中生提供有价值的资讯
2022四川高考数学试题及答案解析
一、选择题(5×12=60分)
1、设集合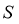 ={
={ |
|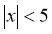 },
}, ={
={ |
| }.则
}.则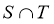 =
=
A. { |-7<
|-7< <-5 } B. {
<-5 } B. { | 3<
| 3<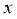 <5 }
<5 }
C. { | -5 <
| -5 <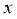 <3} D. {
<3} D. { | -7<
| -7<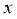 <5 }
<5 }
【答案】C
【解析】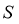 ={
={ |
| },
}, ={
={ |
|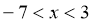 }
}
∴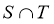 ={
={ | -5 <
| -5 <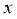 <3}
<3}
2、函数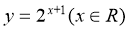 的反函数是
的反函数是
A. 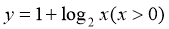 B.
B. 
C.  D.
D. 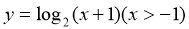
【答案】C
【解析】由 ,又因原函数的值域是
,又因原函数的值域是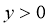 ,
,
∴其反函数是
3、等差数列{ }的公差不为零,首项
}的公差不为零,首项 =1,
=1,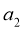 是
是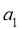 和
和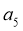 的等比中项,则数列的前10项之和是
的等比中项,则数列的前10项之和是
A. 90 B. 100 C. 145 D. 190
【答案】B
【解析】设公差为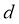 ,则
,则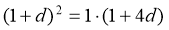 .∵
.∵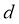 ≠0,解得
≠0,解得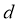 =2,∴
=2,∴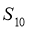 =100
=100
4、已知函数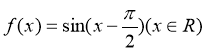 ,下面结论错误的是
,下面结论错误的是
A. 函数 的最小正周期为2
的最小正周期为2 B. 函数
B. 函数 在区间[0,
在区间[0, ]上是增函数
]上是增函数
C.函数 的图象关于直线
的图象关于直线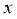 =0对称 D. 函数
=0对称 D. 函数 是奇函数
是奇函数
【答案】D
【解析】∵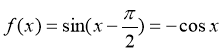 ,∴A、B、C均正确,故错误的是D
,∴A、B、C均正确,故错误的是D
【易错提醒】利用诱导公式时,出现符号错误。
5、设矩形的长为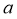 ,宽为
,宽为 ,其比满足
,其比满足 ∶
∶ =
= ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A. 甲批次的总体平均数与标准值更接近
B. 乙批次的总体平均数与标准值更接近
C. 两个批次总体平均数与标准值接近程度相同
D. 两个批次总体平均数与标准值接近程度不能确定
【答案】A
【解析】甲批次的平均数为0.617,乙批次的平均数为0.613
【备考提示】用以上各数据与0.618(或0.6)的差进行计算,以减少
计算量,说明多思则少算。
6、如图,已知六棱锥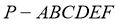 的底面是正六边形,
的底面是正六边形,
 则下列结论正确的是
则下列结论正确的是
A. 
B. 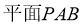
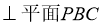
C. 直线 ∥
∥
D. 直线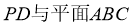 所成的角为45°
所成的角为45°
【答案】D
【解析】∵AD与PB在平面的射影AB不垂直,所以A不成立,又,平面PAB⊥平面PAE,所以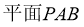
 也不成立;BC∥AD∥平面PAD, ∴直线
也不成立;BC∥AD∥平面PAD, ∴直线 ∥
∥ 也不成立。在
也不成立。在 中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
7、已知 ,
, ,
, ,
,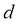 为实数,且
为实数,且 >
> .则“
.则“ >
> ”是“
”是“ -
- >
> -
- ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】B
【解析】显然,充分性不成立.又,若 -
- >
> -
- 和
和 >
> 都成立,则同向不等式相加得
都成立,则同向不等式相加得 >
>
即由“ -
- >
> -
- ”
”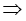 “
“ >
> ”
”
8、已知双曲线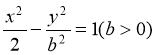 的左、右焦点分别是
的左、右焦点分别是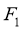 、
、 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点
 在双曲线上.则
在双曲线上.则 ·
·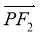 =
=
A. -12 B. -2 C. 0 D. 4
【答案】C
【解析】由渐近线方程为 知双曲线是等轴双曲线,∴双曲线方程是
知双曲线是等轴双曲线,∴双曲线方程是 ,于是两焦点坐标分别是(-2,0)和(2,0),且
,于是两焦点坐标分别是(-2,0)和(2,0),且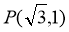 或
或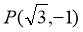 .不妨去
.不妨去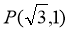 ,则
,则 ,
,
 .∴
.∴ ·
·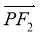 =
=
9、如图,在半径为3的球面上有 三点,
三点, =90°,
=90°, ,
,
 球心O到平面
球心O到平面 的距离是
的距离是 ,则
,则 两点的球面距离是
两点的球面距离是
A.  B.
B. 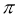
C. 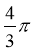 D.2
D.2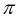
【答案】B
【解析】∵AC是小圆的直径。所以过球心O作小圆的垂线,垂足O’是AC的中点。
O’C= ,AC=3
,AC=3 ,∴BC=3,即BC=OB=OC。∴
,∴BC=3,即BC=OB=OC。∴
,则 两点的球面距离=
两点的球面距离=
10、某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么该企业可获得最大利润是
A. 12万元 B. 20万元 C. 25万元 D. 27万元
【答案】D
| A原料 | B原料 |
甲产品 | 3 | 2 |
乙产品 | | 3 |
则有:
目标函数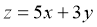
作出可行域后求出可行域边界上各端点的坐标,经验证知:
当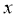 =3,
=3, =5时可获得最大利润为27万元,故选D
=5时可获得最大利润为27万元,故选D
11、2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是
A. 60 B. 48 C. 42 D. 36
【答案】B
【解析】解法一、从3名女生中任取2人“捆”在一起记作A,(A共有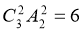 种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;则男生甲必须在A、B之间(若甲在A、B两端。则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求)此时共有6×2=12种排法(A左B右和A右B左)最后再在排好的三个元素中选出四个位置插入乙,所以,共有12×4=48种不同排法。
种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;则男生甲必须在A、B之间(若甲在A、B两端。则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求)此时共有6×2=12种排法(A左B右和A右B左)最后再在排好的三个元素中选出四个位置插入乙,所以,共有12×4=48种不同排法。
解法二;同解法一,从3名女生中任取2人“捆”在一起记作A,(A共有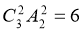 种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;为使男生甲不在两端可分三类情况:
种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;为使男生甲不在两端可分三类情况:
第一类:女生A、B在两端,男生甲、乙在中间,共有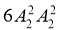 =24种排法;
=24种排法;
第二类:“捆绑”A和男生乙在两端,则中间女生B和男生甲只有一种排法,此时共有 =12种排法
=12种排法
第三类:女生B和男生乙在两端,同样中间“捆绑”A和男生甲也只有一种排法。
此时共有 =12种排法
=12种排法
三类之和为24+12+12=48种。
12、已知函数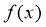 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数 都有
都有
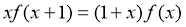 ,则
,则 的值是
的值是
A. 0 B.  C. 1 D.
C. 1 D. 
【答案】A
【解析】若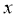 ≠0,则有
≠0,则有 ,取
,取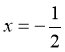 ,则有:
,则有:
 (∵
(∵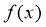 是偶函数,则
是偶函数,则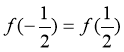 )
)
由此得
于是,
2009年普通高等学校招生全国统一考试(四川卷)
数 学(文史类)
第Ⅱ卷
考生注意事项:
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.抛物线 的焦点到准线的距离是 .
的焦点到准线的距离是 .
【答案】2
【解析】焦点 (1,0),准线方程
(1,0),准线方程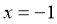 ,∴焦点到准线的距离是2
,∴焦点到准线的距离是2
14. 的展开式的常数项是 (用数字作答)w.w.w.k.s.5.u.c.o.
的展开式的常数项是 (用数字作答)w.w.w.k.s.5.u.c.o.
m 【答案】-20
【解析】 ,令
,令 ,得
,得
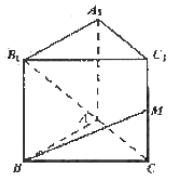 故展开式的常数项为
故展开式的常数项为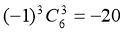
15.如图,已知正三棱柱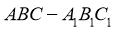 的各条棱长都相等,
的各条棱长都相等, 是侧棱
是侧棱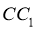 的中点,则异面直线
的中点,则异面直线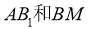 所成的角的大小是 。w.w.w.k.s.5.u.c.o.m
所成的角的大小是 。w.w.w.k.s.5.u.c.o.m
【答案】90°
【解析】作BC的中点N,连接AN,则AN⊥平面BCC1B1,
连接B1N,则B1N是AB1在平面BCC1B1的射影,
∵B1N⊥BM,∴AB1⊥BM.即异面直线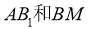 所成的角的大小是90°
所成的角的大小是90°
16.设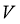 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射 ,记
,记 的象为
的象为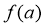 。若映射
。若映射 满足:对所有
满足:对所有 及任意实数
及任意实数 都有
都有 ,则
,则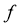 称为平面
称为平面 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设 是平面
是平面 上的线性变换,
上的线性变换, ,则
,则
②若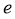 是平面
是平面 上的单位向量,对
上的单位向量,对 ,则
,则 是平面
是平面 上的线性变换;
上的线性变换;
③对 ,则
,则 是平面
是平面 上的线性变换;
上的线性变换;
④设 是平面
是平面 上的线性变换,
上的线性变换,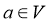 ,则对任意实数
,则对任意实数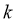 均有
均有 。
。
其中的真命题是 (写出所有真命题的编号)
【答案】①③④
【解析】①:令 ,则
,则 故①是真命题
故①是真命题
同理,④:令 ,则
,则 故④是真命题
故④是真命题
③:∵ ,则有
,则有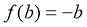
 是线性变换,故③是真命题
是线性变换,故③是真命题
②:由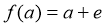 ,则有
,则有

∵ 是单位向量,
是单位向量, ≠0,故②是假命题
≠0,故②是假命题
【备考提示】本小题主要考查函数,对应及高等数学线性变换的相关知识,试题立意新颖,突出创新能力和数学阅读能力,具有选拔性质。
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分12分)
在 中,
中, 为锐角,角
为锐角,角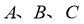 所对的边分别为
所对的边分别为 ,且
,且
(I)求 的值;
的值;
(II)若 ,求
,求 的值。
的值。
【解析】(I)∵ 为锐角,
为锐角,
∴ 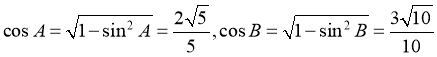

∵ 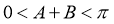
∴  …………………………………………6分
…………………………………………6分
(II)由(I)知 ,∴
,∴ 
由 得
得
 ,即
,即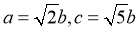
又∵ 
∴ 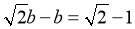 ∴
∴ 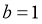
∴  …………………………………………12分
…………………………………………12分
18. (本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有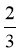 持银卡。w.w.w.k.s.5.u.c.o.m
持银卡。w.w.w.k.s.5.u.c.o.m 

(I)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(II)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率.
【解析】I)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
设事件A为“采访该团2人,恰有1人持银卡”,则

所以采访该团2人,恰有1人持银卡的概率是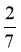 . …………………………………6分
. …………………………………6分
(II)设事件B为“采访该团2人,持金卡人数与持银卡人数相等”,可以分为:
事件B1为“采访该团2人,持金卡0人,持银卡0人”,或事件B2为“采访该团2人,持金卡1人,持银卡1人”两种情况,则

所以采访该团2人,持金卡与持银卡人数相等的概率是 . ……………………12分
. ……………………12分
 19(本小题满分12分)
19(本小题满分12分)
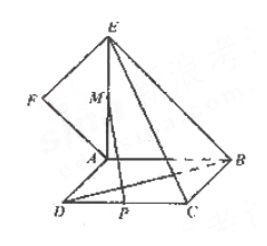
如图,正方形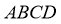 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△ 是等腰直角三角形,
是等腰直角三角形,
(I)求证: ;
;
(II)设线段 、
、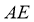 的中点分别为
的中点分别为 、
、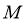 ,求证:
,求证: 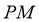 ∥
∥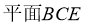
(III)求二面角 的大小。
的大小。
【解析】解法一:
因为平面ABEF⊥平面ABCD,BC 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF.
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE.
因为BC 平面ABCD, BE
平面ABCD, BE 平面BCE,
平面BCE,
BC∩BE=B
所以
…………………………………………6分
(II)取BE的中点N,连结CN,MN,则MN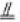

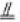 PC
PC
∴ PMNC为平行四边形,所以PM∥CN.
∵ CN在平面BCE内,PM不在平面BCE内,
∴ PM∥平面BCE. …………………………………………8分
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角.
∵ FA=FE,∠AEF=45°,
∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF= ,则
,则
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+ =
= ,
,
 , w.w.w.k.s.5.u.c.o.m
, w.w.w.k.s.5.u.c.o.m 

在Rt⊿FGH中, 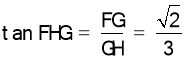 ,
,
∴ 二面角 的大小为
的大小为
…………………………………………12分w.w.w.k.s.5.u.c.o.m 

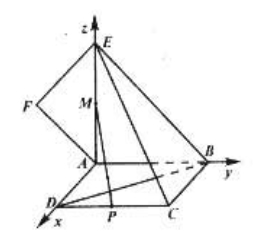
解法二: 因 等腰直角三角形,
等腰直角三角形,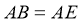 ,所以
,所以
又因为平面 ,所以
,所以 ⊥平面
⊥平面 ,所以
,所以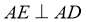
即 两两垂直;如图建立空间直角坐标系,
两两垂直;如图建立空间直角坐标系,
 (I) 设
(I) 设 ,则
,则 ,
,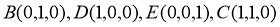
∵ ,∴
,∴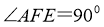 ,
,
从而 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

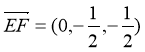 ,
,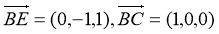
于是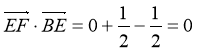 ,
,
∴
 ⊥
⊥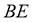 ,
, ⊥
⊥
∵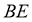
 平面
平面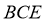 ,
,
 平面
平面 ,
,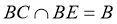
∴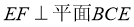
(II) ,从而
,从而
于是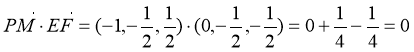
∴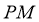 ⊥
⊥ ,又
,又 ⊥平面
⊥平面 ,直线
,直线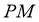 不在平面
不在平面 内,
内,
故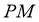 ∥平面
∥平面
(III)设平面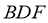 的一个法向量为
的一个法向量为 ,并设
,并设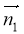 =(
=(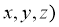

 即
即
取 ,则
,则 ,
, ,从而
,从而 =(1,1,3)
=(1,1,3)
取平面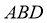 D的一个法向量为
D的一个法向量为
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

故二面角 的大小为
的大小为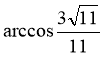
20(本小题满分12分)
已知函数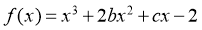 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是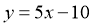 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.
【解析】(I)由已知,切点为(2,0),故有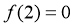 ,即
,即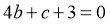 ……①
……①
又 ,由已知
,由已知 得
得 ……②
……②
联立①②,解得 .
.
所以函数的解析式为 …………………………………4分
…………………………………4分
(II)因为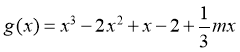
令
当函数有极值时,则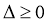 ,方程
,方程 有实数解,w.w.w.k.s.5.u.c.o.m
有实数解,w.w.w.k.s.5.u.c.o.m 

由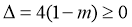 ,得
,得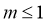 .
.
①当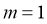 时,
时,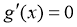 有实数
有实数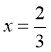 ,在
,在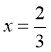 左右两侧均有
左右两侧均有 ,故函数
,故函数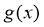 无极值
无极值
②当 时,
时,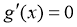 有两个实数根
有两个实数根
 情况如下表:
情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以在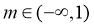 时,函数
时,函数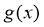 有极值;
有极值;
当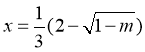 时,
时,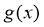 有极大值;当
有极大值;当 时,
时,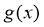 有极小值;
有极小值;
…………………………………12分
21. (本小题满分12分)w.w.w.k.s.5.u.c.o.m 

已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率 ,右准线方程为
,右准线方程为 。
。
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于
与该椭圆交于 两点,且
两点,且 ,求直线
,求直线 的方程。
的方程。
【解析】(I)由已知得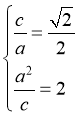 ,解得
,解得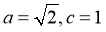 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

∴ 
∴ 所求椭圆的方程为 …………………………………4分
…………………………………4分
(II)由(I)得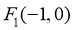 、
、
①若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 ,由
,由 得
得
设 、
、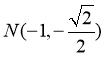 ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m 

∴ 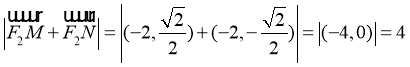 ,这与已知相矛盾。
,这与已知相矛盾。
②若直线 的斜率存在,设直线直线
的斜率存在,设直线直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为
的方程为 ,
,
设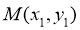 、
、 ,
,
联立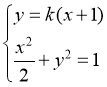 ,消元得
,消元得
∴  ,
,
∴  ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m 

又∵
∴ 
∴ 
化简得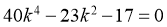
解得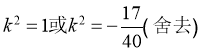
∴ 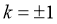
∴ 所求直线 的方程为
的方程为 …………………………………12分
…………………………………12分
22. (本小题满分14分)
设数列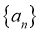 的前
的前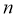 项和为
项和为 ,对任意的正整数
,对任意的正整数 ,都有
,都有 成立,记
成立,记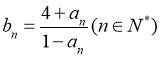 。w.w.w.k.s.5.u.c.o.m
。w.w.w.k.s.5.u.c.o.m 

(I)求数列 与数列
与数列 的通项公式;
的通项公式;
(II)设数列 的前
的前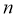 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记 ,设数列
,设数列 的前
的前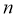 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数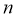 都有
都有 ;
;
【解析】(I)当 时,
时, w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

又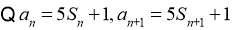
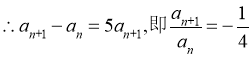
∴数列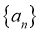 是首项为
是首项为 ,公比为
,公比为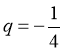 的等比数列,
的等比数列,
∴ ,
, …………………………………3分
…………………………………3分
(II)不存在正整数 ,使得
,使得 成立。
成立。
证明:由(I)知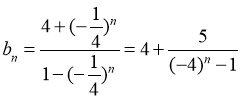 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 


∴当n为偶数时,设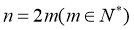 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

∴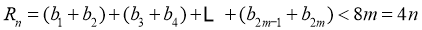
当n为奇数时,设
∴
∴对于一切的正整数n,都有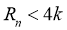 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

∴不存在正整数 ,使得
,使得 成立。 …………………………………8分
成立。 …………………………………8分
(III)由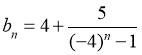 得w.w.w.k.s.5.u.c.o.m
得w.w.w.k.s.5.u.c.o.m 

 又
又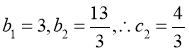 ,w.w.w.k.s.5.u.c.o.m
,w.w.w.k.s.5.u.c.o.m 

当 时,
时, ,
,
当 时,
时,
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m 

…………………………………14分

Copyright 2019-2029 http://www.laigaokao.com 【来高考】 皖ICP备19022700号-4
声明: 本站 所有软件和文章来自互联网 如有异议 请与本站联系 本站为非赢利性网站 不接受任何赞助和广告