以P为切点的切线方程：y-f(a)=f'(a)(x-a)；若过P另有曲线C的切线，切点为Q(b,f(b))，则切线为y-f(a)=f'(b)(x-a)，也可y-f(b)=f'(b)(x-b)，并且[f(b)-f(a)]/(b-a)=f'(b)。

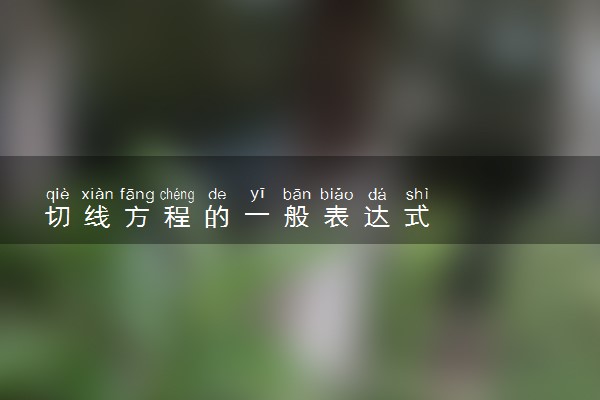
切线方程是研究切线以及切线的斜率方程，涉及几何、代数、物理向量、量子力学等内容。是关于几何图形的切线坐标向量关系的研究。分析方法有向量法和解析法。

1、如果某点在曲线上：

设曲线方程为y=f(x)，曲线上某点为(a，f(a))

求曲线方程求导，得到f'(x)，

将某点代入，得到f'(a)，此即为过点(a，f(a))的切线斜率，

由直线的点斜式方程，得到切线的方程。y-f(a)=f'(a)(x-a)

2、如果某点不在曲线上：

设曲线方程为y=f(x)，曲线外某点为(a，b)

求对曲线方程求导，得到f'(x)

设：切点为(x0，f(x0))，

将x0代入f'(x)，得到切线斜率f'(x0)，

由直线的点斜式方程，得到切线的方程y-f(x0)=f'(x0)(x-x0)，

因为(a，b)在切线上，代入求得的切线方程，

有：b-f(x0)=f'(x0)(a-x0)，得到x0，

代回求得的切线方程，即求得所求切线方程。