统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数；标准差是总体各单位标准值与其平均数离差平方的算术平均数的平方根。

方差、标准差、协方差的区别

1、概念不同

统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数；标准差是总体各单位标准值与其平均数离差平方的算术平均数的平方根；协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。

2、计算方法不同

方差的计算公式为：

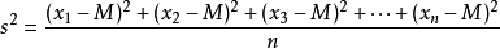
式中的s²表示方差，x1、x2、x3、.......、xn表示样本中的各个数据，M表示样本平均数；

标准差=方差的算术平方根=s=sqrt(((x1-x)^2+(x2-x)^2+......(xn-x)^2)/n)；

协方差计算公式为：Cov(X,Y)=E[XY]-E[X]E[Y]，其中E[X]与E[Y]是两个实随机变量X与Y的期望值。

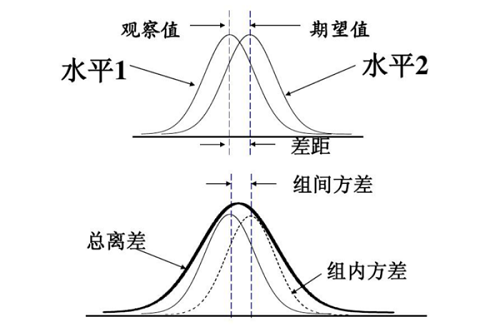
3、意义不同

方差和标准差都是对一组(一维)数据进行统计的，反映的是一维数组的离散程度；

而协方差是对2组数据进行统计的，反映的是2组数据之间的相关性。

方差、标准差、和协方差之间的联系与区别

１.方差和标准差都是对一组（一维）数据进行统计的，反映的是一维数组的离散程度；而协方差是对2维数据进行的，反映的是2组数据之间的相关性。

２.标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。方差可以看成是协方差的一种特殊情况，即2组数据完全相同。

３.协方差只表示线性相关的方向，取值正无穷到负无穷。

４.协方差只是说明了线性相关的方向，说不能说明线性相关的程度，若衡量相关程度，则使用相关系数。