在数学中，二次函数最高次必须为二次，二次函数表示形式为y=ax²+bx+c（a≠0)的多项式函数。二次函数的图像是一条对称轴平行于y轴的抛物线。

定义与定义表达式

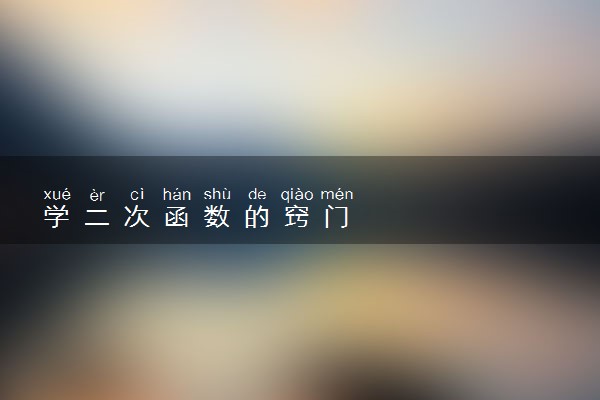
一般地，自变量x和因变量y之间存在如下关系：y=ax²+bx+c

（a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.）则称y为x的二次函数。

二次函数的三种表达式

一般式：y=ax²+bx+c（a，b，c为常数，a≠0）

顶点式：y=a(x-h)²+k[抛物线的顶点P（h，k）]

交点式：y=a(x-x₁)(x-x₂)[仅限于与x轴有交点A（x₁，0）和B（x₂，0）的抛物线]

注：在3种形式的互相转化中，有如下关系:

h=-b/2ak=(4ac-b²)/4ax₁,x₂=(-b±√b²-4ac)/2a

二次函数图像与X轴交点的情况

当△=b²-4ac>0时，函数图像与x轴有两个交点。

当△=b²-4ac=0时，函数图像与x轴只有一个交点。

当△=b²-4ac<0时，函数图像与x轴没有交点。

二次函数的应用

1、二次函数的图象、性质广泛应用于实际生活中，主要有最大利益的获取，最佳方案的设计、最大面积的计算等问题。

2、解决最值问题的基本思路：(1)认真审题，分清题中的已知和未知，找出数量间的关系；(2)确定自变量x及函数y；(3)根据题中实际数量的相等关系，建立函数关系模型；(4)分析表信息、利用待定系数法、配方法等求出最值。